By Gustavo Luyo
Guessing in order to find the answer to a question does not sound especially appealing if the question is one about mathematics in an international examination, let alone the GMAT quantitative section. However, ballparking, or estimating an answer in an educated manner when solving the multiple-choice question format in the GMAT quantitative section is not as bold as it might look like. Here we will consider a few examples that demonstrate how this technique combined with actual clever solving can give you a boost when trying to beat time-hungry GMAT math problems:

First, let’s analyze what is required to solve the problem: repeating decimals can be represented with fractions having just 9s in the denominator, for example, 0.111… = 1/9 and 0.232323… = 23/99. We know that if the fractions in the answer choices had all of them just the digit 9 any number of times in the denominators the answer would simply be the fraction with the most 9s in the denominator. However, what would happen if two different fractions in the answer choices had the same quantity of 9s? That would automatically invalidate such two choices, since there is no possibility of having more than one correct answer choice in the problem-solving question format.
Let us apply this reasoning to the question above: first answer choice 2/11 is easily shaped into an equivalent fraction with just 9s in the denominator, namely 18/99, but so is third answer choice 41/99. Both have a repeating decimal sequence of length 2, and as both cannot be the right answer choice at the same time, we know we can rule out both choices. Likewise, both second choice 1/3 and fourth choice 2/3 can become fractions with just one 9 in the denominator. Logically, neither of these two can be the right answer choice, either. Inevitably we need to turn our attention to the fifth answer choice. As we have already ruled out the other four answer choices, the certainty that a unique answer must exist would compel us to mark the fifth option for an answer. The correct fraction MUST have a decimal digit sequence longer than 1 and 2, whichever fraction that is. Notice that ballparking the right answer in this way rids us of the necessity to find the exact length of the longest decimal digit sequence, which we cannot know unless we first undertake the daunting task of finding the exact equivalent fraction of 23/37, and then count the number of 9s in its denominator.
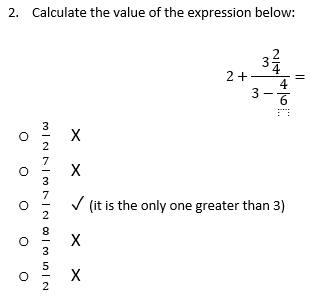
Instead of rushing to do the math (not that it is that hard, either), we can beat the clock if we just remain vigilant of the fact that any improper fraction is always greater than 1. Thus, the second term in the expression looks like an improper fraction, since the numerator is clearly greater than the denominator (the numerator is obviously greater than 3, and the denominator is less than 3). If we added 2 (the first term of the expression) and a number greater than 1, the result must be greater than 3. We can now rule out answer choices (1), (2), (4), and (5), for none of them is greater than three. Notice that we did NOT actually calculated the value, but ballparked it.
Ballparking can help you work your way around some tedious and time-consuming calculations in the GMAT Quant section. Remain alert to detecting problems where you can try this approach, and consider this technique as one more option to keep in your bag of tricks.